OpenCV Sobel衍生物
2021-02-19 17:02 更新
目标
在本教程中,您将学习如何:
- 使用 OpenCV 函数
cv :: Sobel 来计算图像中的衍生物。 - 使用 OpenCV 函数
cv :: Scharr 计算 3 \ cdot 3 的内核的更准确的导数 3⋅3
理论
- 注意
- 下面的解释属于 Bradski 和 Kaehler 的《学习 OpenCV 》一书。
- 在最后两个教程中,我们已经看到了卷积的应用例子。最重要的卷积之一是计算图像中的导数(或与其近似)。
- 为什么在图像中派生物的演算可能很重要?让我们想象一下,我们想要检测图像中存在的边。例如:

你可以很容易地注意到,在边缘,像素强度以臭名昭着的方式发生变化。表达变化的一个好方法是使用衍生工具。梯度的高变化表示图像的重大变化。
- 为了更加图形化,我们假设我们有一个 1D 图像。在下面的图中,边缘以强度显示为“跳跃”
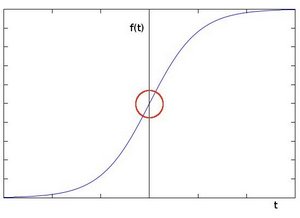
- 如果我们采用一阶导数(实际上,这里显示为最大值),边缘“跳”可以更容易看到
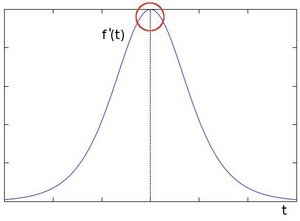
- 因此,从上面的解释,我们可以推断出,通过定位梯度高于邻居的像素位置(或者概括为高于阈值),可以执行检测图像边缘的方法。
- 更详细的解释,请参考 Bradski 和 Kaehler 学习 OpenCV
Sobel 操作
- Sobel 运算符是一个离散差分运算符。它计算图像强度函数的梯度的近似值。
- Sobel 算子结合高斯平滑和微分。
公式
假设要运行的图像是:I
- 我们计算两个派生词:
- 水平变化:这是通过卷积计算与内核具有奇数大小。例如,对于内核大小为3,将计算为:IGxGx
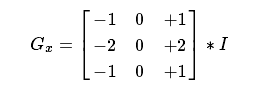
- 垂直变化:这是通过卷积计算与内核具有奇数大小。例如,对于内核大小为3,将被计算为: 一世 Gÿ Gÿ
- 在图像的每个点,我们通过组合上述两个结果来计算该点的渐变近似值:
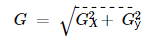
虽然有时使用以下简单的方程:
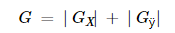
3,上面显示的 Sobel 内核可能会产生明显的不准确(毕竟 Sobel 只是导数的近似值)。OpenCV 通过使用 cv :: Scharr 函数解决了大小为 3 的内核的不精确性。这与标准的 Sobel 功能一样快,但更准确。它实现以下内核:
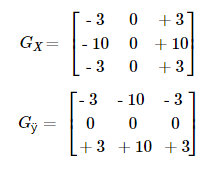
您可以在 OpenCV 参考(cv :: Scharr)中查看此功能的更多信息。此外,在下面的示例代码中,您会注意到,在 cv :: Sobel 函数的代码之上,还有一个注释的cv :: Scharr函数的代码。取消注释(并且显然评论 Sobel 的内容)应该给你一个这个功能如何工作的想法。
Code
- 这个程序是做什么的?应用 Sobel 操作员,并生成作为输出的图像,检测到的边缘在较暗的背景上亮起。
- 教程代码如下所示。您也可以从这里下载
#include "opencv2/imgproc.hpp"
#include "opencv2/imgcodecs.hpp"
#include "opencv2/highgui.hpp"
using namespace cv;
int main( int argc, char** argv )
{
Mat src, src_gray;
Mat grad;
const char* window_name = "Sobel Demo - Simple Edge Detector";
int scale = 1;
int delta = 0;
int ddepth = CV_16S;
String imageName("../data/lena.jpg");
// 默认情况下
if (argc > 1)
{
imageName = argv[1];
}
src = imread( imageName, IMREAD_COLOR );
// 加载一张图片
if( src.empty() )
{
return -1;
}
GaussianBlur( src, src, Size(3,3), 0, 0, BORDER_DEFAULT );
cvtColor( src, src_gray, COLOR_BGR2GRAY );
Mat grad_x, grad_y;
Mat abs_grad_x, abs_grad_y;
//Scharr( src_gray, grad_x, ddepth, 1, 0, scale, delta, BORDER_DEFAULT );
Sobel( src_gray, grad_x, ddepth, 1, 0, 3, scale, delta, BORDER_DEFAULT );
//Scharr( src_gray, grad_y, ddepth, 0, 1, scale, delta, BORDER_DEFAULT );
Sobel( src_gray, grad_y, ddepth, 0, 1, 3, scale, delta, BORDER_DEFAULT );
convertScaleAbs( grad_x, abs_grad_x );
convertScaleAbs( grad_y, abs_grad_y );
addWeighted( abs_grad_x, 0.5, abs_grad_y, 0.5, 0, grad );
imshow( window_name, grad );
waitKey(0);
return 0;
}说明
- 首先我们声明我们要使用的变量:
Mat src, src_gray;
Mat grad;
const char* window_name = "Sobel Demo - Simple Edge Detector";
int scale = 1;
int delta = 0;
int ddepth = CV_16S;- 像往常一样,我们加载我们的源图像
src:
String imageName("../data/lena.jpg");
// 默认情况下
if (argc > 1)
{
imageName = argv[1];
}
src = imread( imageName, IMREAD_COLOR );
// 加载一张图片
if( src.empty() )
{
return -1;
}- 首先,我们将
cv :: GaussianBlur应用于我们的图像以减少噪声(内核大小= 3)
GaussianBlur( src, src, Size(3,3), 0, 0, BORDER_DEFAULT );- 现在我们将过滤的图像转换为灰度:
cvtColor(src,src_gray,COLOR_BGR2GRAY);- 其次,我们在 x 和 y 方向计算“*导数*” 。为此,我们使用函数
cv :: Sobel,如下所示:
Mat grad_x, grad_y;
Mat abs_grad_x, abs_grad_y;
//Scharr( src_gray, grad_x, ddepth, 1, 0, scale, delta, BORDER_DEFAULT );
Sobel( src_gray, grad_x, ddepth, 1, 0, 3, scale, delta, BORDER_DEFAULT );
//Scharr( src_gray, grad_y, ddepth, 0, 1, scale, delta, BORDER_DEFAULT );
Sobel( src_gray, grad_y, ddepth, 0, 1, 3, scale, delta, BORDER_DEFAULT );该函数采用以下参数:
-
src_gray:在我们的示例中,输入图像。这里是CV_8U; -
grad_x / * grad_y *:输出图像; -
ddepth:输出图像的深度。我们将其设置为CV_16S以避免溢出; -
x_order:x方向上导数的顺序; -
y_order:y方向上导数的顺序; -
scale,delta和BORDER_DEFAULT:我们使用默认值。
请注意,为了计算x方向的梯度,我们使用:
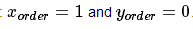 。我们以
。我们以y方式做类似的事情。
- 我们将部分结果转换回
CV_8U:
convertScaleAbs(grad_x,abs_grad_x);
convertScaleAbs(grad_y,abs_grad_y);最后,我们试图接近梯度通过将两个方向的梯度(注意,这是不是在所有的精确计算!但它有利于我们的目的)。
addWeighted(abs_grad_x,0.5,abs_grad_y,0.5,0,grad);
最后,我们展示我们的结果:
imshow(window_name,grad);
waitKey(0);结果
这是将我们的基本检测器应用于lena.jpg的输出:

以上内容是否对您有帮助:





更多建议: