哈夫曼编码
哈夫曼编码(Huffman Coding),又称霍夫曼编码,是一种编码方式,哈夫曼编码是可变字长编码(VLC)的一种。Huffman于1952年提出一种编码方法,该方法完全依据字符出现概率来构造异字头的平均长度最短的码字,有时称之为最佳编码,一般就叫做Huffman编码(有时也称为霍夫曼编码)。
定理
在变字长编码中,如果码字长度严格按照对应符号出现的概率大小逆序排列,则其平 均码字长度为最小。 现在通过一个实例来说明上述定理的实现过程。设将信源符号按出现的概率大小顺序排列为 : U: ( a1 a2 a3 a4 a5 a6 a7 ) [1] 0.20 0.19 0.18 0.17 0.15 0.10 0.01 给概率最小的两个符号a6与a7分别指定为“1”与“0”,然后将它们的概率相加再与原来的 a1~a5组合并重新排序成新的原为: U′: ( a1 a2 a3 a4 a5 a6′ ) 0.20 0.19 0.18 0.17 0.15 0.11 对a5与a′6分别指定“1”与“0”后,再作概率相加并重新按概率排序得 U″:(0.26 0.20 0.19 0.18 0.17)… 直到最后得 U″″:(0.61 0.39) 赫夫曼编码的具体方法:先按出现的概率大小排队,把两个最小的概率相加,作为新的概率 和剩余的概率重新排队,再把最小的两个概率相加,再重新排队,直到最后变成1。每次相 加时都将“0”和“1”赋与相加的两个概率,读出时由该符号开始一直走到最后的“1”, 将路线上所遇到的“0”和“1”按最低位到最高位的顺序排好,就是该符号的赫夫曼编码。 例如a7从左至右,由U至U″″,其码字为1000; a6按路线将所遇到的“0”和“1”按最低位到最高位的顺序排好,其码字为1001… 用赫夫曼编码所得的平均比特率为:Σ码长×出现概率 上例为:0.2×2+0.19×2+0.18×3+0.17×3+0.15×3+0.1×4+0.01×4=2.72 bit 可以算出本例的信源熵为2.61bit,二者已经是很接近了。
例子
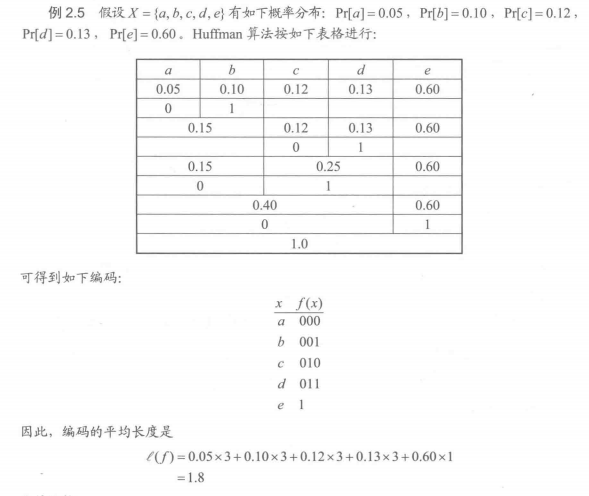






更多建议: