canvas动画包教不包会:缓动与弹动
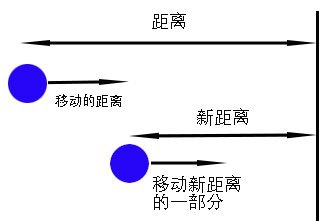
- 有一个目标点
- 确定物体到目标点的距离
- 运动与距离是成正比的----距离越远,运动的程度越大
- 运动和距离成正比的方式不一样。缓动是指 速度 与 距离 成正比(物体离目标越远,物体运动的速度越快,当物体运动到很接近目标点时,物体几乎就停下来了);而弹动是指 加速度 与 距离 成正比(物体离目标点越远,加速度就快速增大,当物体很接近目标点时,加速度变得很小,但它还是在加速;当它越过目标点之后,随着距离的变大,反向加速度也随之变大,就会把它拉回了,最终在摩擦力的作用下停住。)
- 为运动确定一个小于1且大于0的小数作为比例系数(easing)
- 确定目标点
- 计算物体与目标点的距离
- 计算速度,速度=距离 * 比例系数
- 用当前位置加上速度来计算新的位置
- 不断重复第3步到第5步,直到物体到达目标点
dx = targetX - ball.x;
dy = targetY - ball.y;
easing = vx / dx; => vx = dx * easing;
easing = vy / dy; => vy = dy * easing;
ball.x += vx; => ball.x += dx*easing; => ball.x += (targetX - ball.x) * easing;
ball.y += vy; => ball.y += dy*easing; => ball.y += (targetY - ball.y) * easing;
ball.x += (targetX - ball.x) * easing;
ball.y += (targetY - ball.y) * easing;
关键代码:
var easing = 0.05;
var targetX = canvas.width - 10;
var targetY = canvas.height - 10;
在上面的例子中,我们将比例系数设为0.05,用变量easing表示,然后在循环中调用下面的代码:
ball.x += (targetX- ball.x)*easing; //每次循环中调用
这样简单的处理,就能实现刹车模式,这就是缓动的一种效果,你可以改变easing看看。
上面的例子中的目标点是canvas边界,其实,目标点是可以 变动 的,因为我们每次都会重新计算距离,所以只须在播放每一帧的时候知道目标点的位置,然后就可以计算距离和速度了。比如:将鼠标位置(mouse.x和mouse.y)作为目标点,你可以试试,会发现鼠标里的越远,小球就运动的越快。
这里还有一个关键性问题:何时停止缓动
不是到达目标点就停止缓动吗?估计这是你看到这的第一想法,你还可能立即想到下面判断公式:
if(ball.x === targetX && ball.y === targetY){
//到达目标点
}
这是理论上的判断,但是从数学的角度来看,下面的公式永远不会相等:
(ball.x + (targetX - ball.x) * easing) !== targetX
这是为什么呢?
这就涉及了 芝诺饽论 ,简单的理解是这样:为了把一个物体从A点移到B点,就必须把它先移到到A和B的中间点C,然后再移到C和B的中间点,然后再折半,不断地重复下去,每次移到到物体到距离目标点的一半,这样就会进入无穷循环下去,物体永远不会到达目标点。
我们来看看数学例子:物体从0的位置,要将它移到100,比例系数easing设为0.,5,然后将它每次移动距离的一半,过程如下:
- 从原点开始,在第一帧后,它移到到50
- 在第二帧后,移动到75
- 在第三帧后,移动到87.5
- 就这样循环下去,物体位置变化是93.75、96.875等,经过20帧后,它的位置是99.999809265
看到没有,它会离目标点越来越近,可是理论上是永远不会到达目标点的,所以上面的判断公式是永远不会返回true的。
但毕竟肉眼是无法分辨这么精确的位置变化的,有时候当ball.x 等于99的时候,我们在canvas上看就已经是到达终点了,所以这就产生了一个问题:多近才是足够近呢?
这就需要我们人为的指定一个特定值,判断物体到目标点的距离是否小于特定值,如果小于特定值,那我们就认为它到达终点了。
/*二维坐标*/
distance = Math.sqrt(dx * dx + dy * dy);
/*一维坐标*/
distance = Math.abs(dx)
if(distance < 1){
console.log('到达终点');
cancelAnimationFrame(requestID);
}
一般采取是否小于1来判断是否到达目标点,是为了停止动画,避免资源的浪费。
在tool.js工具类中,我们已经封装了停止 requestAnimaitonFrame 动画的方法,就是 cancelRequestAnimationFrame ,参数是requestID。
var cancelAnimationFrame = function() {
return window.cancelAnimationFrame || window.webkitCancelAnimationFrame || window.mozCancelAnimationFrame || function(id) {
clearTimeout(id);
};
}();
当然,缓动并不仅仅适用于运动,它还可以应用很多属性:
(1)旋转
定义起始角度:
var rotation = 0;
var targetRotation = 360;
然后缓动:
rotation += (targetRotation - rotation) * easing;
object.rotation = rotation * Math.PI / 180;
别忘了弧度与角度的转换。
(2)透明度
设置起始透明度
var alpha = 0;
var targetAlpha = 1;
设置缓动:
alpha += (targetAlpha - alpha) * easing;
object.color = 'rgba(255,0,0,' + alpha + ')';
2、弹动
前面提到过,在弹动中,物体的 加速度 与它到目标点的 距离 成正比。
现实中的弹动例子:在橡皮筋的一头系上一个小球(悬空,静止时的点就是目标点),另一头固定起来。当我们用力(力足够大)去拉小球然后松开,我们会看到小球反复的上下运动几次后,速度逐渐慢下来,停在目标点上。(没玩过橡皮筋的,可以去实践一下)
2.1 一维坐标上的弹动
实现弹动的代码和缓动类似,只不过将速度换成了加速度(spring)。
var spring = 0.1;
var targetX = canvas.width / 2;
var vx = 0;
计算小球到目标点的距离:
var dx = targetX - ball.x;
计算加速度,与距离是成比例的:
var ax = dx * spring;
将加速度加在速度上,然后添加到小球的位置上:
vx += ax;
ball.x += vx;
我们先模拟一下整个弹动过程,假设小球的x是0,vx也是0,目标点的x是100,spring变量的值为0.1:
- 用距离(100)乘以spring,得到10,将它加在vx上,vx变为10,把vx加在小球的位置上,小球的x为10
- 下一帧,距离(100-10)为90,加速度为90乘以0.1,等于9,加在vx上,vx就变为19,小球的x变为了29
- 再下一帧,距离是71,加速度是7.1,vx是26.1,小球的x为55.1
重复几次后,随着小球一帧一帧的靠近目标,加速度变得越来越小,速度越来越快,虽然增加的幅度在减小,但还是在增加。
当小球越过了目标点,到底了x轴上的117点时,与目标点的距离是-17(100-117)了,也就是加速度会是-1.7,当速度加上这个加速度时,小球就会减速运动。
这就是弹动的过程。
看看实例(目标点定在canvas的中心点,相当于将球从中心点拉到左边,然后松开):
上面的例子中,小球是不是有种被弹簧拉扯的效果,但是,由于小球的摆动幅度不变,它现在貌似停不下来,这不科学,现实中,它的摆动幅度应该是越来越小(由于阻力),弹动的越来越慢,直到停下来,所以为了更真实,我们应该给它添加一个摩擦力friction:
var friction = 0.95;
然后改变速度:
vx += ax;
vx *= friction;
ball.x += vx;
当小球停止时,我们就不需去执行动画了,所以我们还需要判断是否停止:
if(Math.abs(vx) < 0.001){
vx += ax;
vx *= friction;
ball.x += vx;
};
注意:当你的初始速度vx为0时,这样是无法进入弹动的,对我来说,我会加入一个变量判断是否开始弹动:
var isBegin = false;
if(!isBegin || Math.abs(vx) < 0.001){
vx += ax;
vx *= friction;
ball.x += vx;
isBegin = true;
};
2.2 二维坐标上的弹动
二维坐标上的弹动与一维坐标上的弹动并没有大区别,只不过前者多了y轴上的弹动。
初始化变量:
var vx = 0;
var ax = 0;
var vy = 0;
var ay = 0;
var dx = 0;
var dy = 0;
设置x、y轴上的弹动:
if(Math.abs(vx) > 0.001){
dx = targetX - ball.x;
ax = dx * spring;
vx += ax;
vx *= friction;
ball.x += vx;
dy = targetY - ball.y;
ay = dy * spring;
vy += ay;
vy *= friction;
ball.y += vy;
};
例子(将canvas的中心点作为目标点,相当于一开始将球从中心点拉到左上角,然后松开):
上面的例子依旧是一个直线弹动,你可以试试将vx或vy的初始值增大一点,设为50,会有意想不到的动画。
2.3 向移动的目标点弹动
在缓动中也说过,目标点不一定是固定,而对于弹动也一样,目标点可以是移动的,只需在每一帧改变目标点的坐标值即可,比如:鼠标坐标是目标点:
dx = targetX - ball.x;
dy = targetY - ball.y;
/*改成如下*/
dx = mouse.x - ball.x;
dy = mouse.y - ball.y;
2.4 绘制弹簧
在上面的几个例子中,虽然有了弹簧的效果,可是始终还是没看到橡皮筋所在,所以我们有必要来将橡皮筋绘画出来:
ctx.beginPath();
ctx.moveTo(ball.x,ball.y);
ctx.lineTo(mouse.x,mouse.y);
ctx.stroke();
实例:
为了更真实,你还可以加上重力加速度:
var gravity = 2;
vy += gravity;
注意:在物理学中,重力是一个常数,只由你所在星球的质量来决定的。理论上,应该保持gravity值不变,比如0.5,然后给物体增加一个mass(质量)属性,比如10,然后用mass乘以gravity得到5(依旧用gravity变量表示)。
2.5 链式弹动
链式运动是指物体A以物体B为目标点,物体B又以物体C为目标点,诸如此类的运动。
看看例子,然后再来分析:
在上面的例子中,我们创建了四个球,每个球都有自己的属性 vx 和 vy ,初始为0。在动画函数 animation 里,我们使用Array.forEach()方法来绘制每一个球,然后连线。在 connect 方法中,你可以看到第一个球的目标点是鼠标位置,剩余的球都是以上一个球(balles[i-1])的坐标位置为目标点来弹动。
我还给球添加了重力:
ball.vy += gravity;
运动结束时,四个球会连成一串。
2.6 目标偏移量
在上面的所有例子中,我们使用的都是模拟橡皮筋,如果我们模拟的是一个弹性金属材料制作的弹簧会怎样呢?是不是球还可以这样自由的运动呢?
答案是否定,在现实中,你无法让物体顶着弹簧从一头运动到另一头,还不明白?看下图:

假设上面的图中连接球和固定点是金属弹簧,那么球是永远都到不了固定点的位置的,因为弹簧是有体积的,会把球挡住,而且一旦弹簧收缩到它正常的长度,它就不会对小球施加拉力了,所以,真正的目标点,其实是弹簧处于松弛(拉伸)状态时,系着小球那一端的那个点(这个点是变化的)。
那如何确定目标点呢?
其实,从我上面的图你就应该想到,要用三角函数,因为我们知道球的位置、固定点的位置,那我们就可以获得球与固定点之间的夹角 θ ,当然,我们还需要定义一个弹簧的长度(springLength),比如:100。
计算目标点的代码如下:
dx = ball.x - fixedX;
dy = ball.y -fixedY;
angle = Math.atan2(dy,dx);
targetX = fixedX + Math.cos(angle) * springLength;
targetY = fixedY + Math.sin(angle) * springLength;
又到了例子时刻(以canvas的中心点为固定点,弹簧长度为100,小球可拖动):
试过上面例子了吗?我们再来看看上面的图:

图中的A点相当于例子中的固定点(也就是canvas的中心点),B点是弹簧(无压缩无拉伸)正常情况下的位置(也是弹动的目标点),C点就是你拖动小球然后松开鼠标的位置,那么AB之间的距离就是弹簧的长度100,而BC之间的距离就是小球弹动的距离了,同时,基于直角三角形,我们也很容易求得 θ 的值。
我们还定义了一个 getBound() 方法,传入球对象,返回一个矩形对象,也就是球的矩形边界。
例子的部分代码:
dx = ballA.x - mouse.x;
dy = ballA.y - mouse.y;
angle = Math.atan2(dy, dx); // 获取鼠标与球之间的夹角θ
//计算目标点坐标
targetX = mouse.x + Math.cos(angle) * springLength;
targetY = mouse.y + Math.sin(angle) * springLength;
ballA.vx += (targetX - ballA.x) * spring;
ballA.vy += (targetY - ballA.y) * spring;
ballA.vx *= friction;
ballA.vy *= friction;
ballA.x += ballA.vx;
ballA.y += ballA.vy;
2.7 用弹簧连接多个物体
我们还可以用弹簧连接多个物体,先从连接两个物体开始,让它们互相向对方弹动,移动其中一个,另一个就要跟随弹动过去:
上例子:
在上面的例子中,我们创建了两个Ball实例 ball0 和 ball1 ,都是可拖动的,ball0向ball1弹动,ball1向ball0弹动,而且它们之间有一定的偏移量,两者用弹簧连接。
springTo() 方法接受两个参数,第一个参数是移动物体,第二个参数是目标点。还要引入两个变量: ball0_dragging 和 ball1_dragging ,作为是否拖动小球的标志。
if(!ball0_dragging) {
springTo(ball0, ball1);
};
if(!ball1_dragging) {
springTo(ball1, ball0);
};
下面让我们加入第三个球ball2:
总结
本章主要介绍了两个比例运动:缓动和弹动
- 缓动是指 速度 与 距离 成正比(物体离目标越远,物体运动的速度越快,当物体运动到很接近目标点时,物体几乎就停下来了);
- 弹动是指 加速度 与 距离 成正比(物体离目标点越远,加速度就快速增大,当物体很接近目标点时,加速度变得很小,但它还是在加速;当它越过目标点之后,随着距离的变大,反向加速度也随之变大,就会把它拉回了,最终在摩擦力的作用下停住。)
附录
重要公式:
(1)简单缓动
dx = targetX - object.x;
dy = targetY - object.y;
vx = dx * easing;
vy = dy * easing;
object.x += vx;
object.y += vy;
可精简:
vx = (targetX - object.x) * easing;
vy = (targetY - object.y) * easing;
object.x += vx;
object.y += vy;
再精简:
object.x += (targetX - object.x) * easing;
object.y += (targetY - object.y) * easing;
(2)简单弹动
ax = (targetX - object.x) * spring;
ay = (targetY - object.y) * spring;
vx += ax;
vy += ay;
vx *= friction;
vy *= friction;
object.x += vx;
object.y += vy;
可精简:
vx += (targetX - object.x) * spring;
vy += (targetY - object.y) * spring;
vx *= friction;
vy *= friction;
object.x += vx;
object.y += vy;
再精简:
vx += (targetX - object.x) * spring;
vy += (targetY - object.y) * spring;
object.x += (vx *= friction);
object.y += (vy *= friction);
(3)有偏移的弹动
dx = object.x - fixedX;
dy = object.y - fixedY;
targetX = fixedX + Math.cos(angle) * springLength;
targetY = fixedY + Math.sin(angle) * springLength;
下一章:碰撞检测

 免费AI编程助手
免费AI编程助手




更多建议: