运用余数思考
@课前对话:
1,奇数是什么?1,3,5,7,9...奇数就是被2除余1的整数。
2,偶数是什么?能被2整除的整数。
3,除法就像分组,余数来确定它属于哪个组。
(1),例如下边的例子,今天星期日,判断100天以后是星期几,100除以7,将这100天分组,就是14周零2天,星期日过2天,就是星期2,余数判断结果属于星期2组。
(2),自己总结的一个通俗易懂的例子,例如100个学生,老师说每7个人一组,那就用100除以7,这就是分组。例如,一个学生是23号,23除以7余2,那这个学生就是第4组第2号,这就是余数来确定你属于哪个组。除以8,就是8个人一组。
@开始本章学习内容:
1,余数是什么?余数就是作除法运算时剩下的数。
2,无论在数学还是在编程中,余数都起着非常重要的作用。
3,今天是星期日,那么100天以后是星期几?
98是7的倍数,98天后是星期日(98天后,那天就是星期日),99天后是星期一,100天后是星期二。

---运用余数思考:
假设今天是星期日,100天后的星期数就是"100除以7的余数"。
100/7=14余2,因此100天后是星期二。
4,余数的力量---将较大的数字除一次就能分组。
(1),问题:求一亿天后的星期数,靠数数就解决不了问题了。即使1秒数1下,数到1亿至少也要花费3年以上的时间。
而如果运用余数的话,1亿天以后的星期数很快就能算出来。如下所示:
100000000/7=14285714余2
因为余数为2,所以1亿天以后是星期二。
因为余数为2,所以1亿天以后是星期二。
n天后的星期数,可以通过n除以7的余数来判断。因为星期数时以7为周期循环的。
在面对难以直接计算的庞大数字时,只要发现它是如何循环的(即找到它的规律),就能通过余数的力量将其降服。
(2),今天是星期日,那么10^100天以后是星期几?这个数有100个0。
这个数字太大了,计算起来相当费力,即使借助计算器也很难完成。我们找出它循环的规律。

果然有规律呢!余数以1,3,2,6,4,5...的顺序循环,星期数以一,三,二,六,四,五...的顺序循环。这个周期性可以通过笔算较快得出。

我们通过观察发现,每增加6个0,星期数就相同,因此周期为6。将0的个数除以6,得到的余数为0,1,2,3,4,5的其中之一,他们分别对应星期一,星期三,星期二,星期六,星期四,星期五(咦?没有星期日呢)。

因此,10^100天以后的星期数,可以将天数中的0的个数(10^100有100个0)除以6,通过所得的余数来判断。我们来计算一下。
100/6=16余4
余数为4,因此10^100天以后是星期4。
答案:星期四。
(3),发现规律,在上边第一题中,我们借助数字的规律,解答出了星期数。在第二题中,我们找到了0的个数的规律,退出了答案。使用这种方法,就连非常遥远的未来的星期数页可以很快算出来。我们这就试算一下"10^1亿"天以后的星期数。
10^1亿天以后:
100000000/6=16666666余4
余数为4,所以答案是星期四。当然,恐怕到那时宇宙都已经消失了吧......
由此可见,在处理难以计算的超大数字时,发现与之相关的规律是相当重要的。余数可谓是有效利用规律的工具。
5,乘方的思考题:
(1),1234567^987654321的个数是什么呢?
提示:通过试算找出规律。1234567^987654321的值无法用计算器算出来。即使用计算机程序来算,由于位数过多,计算过程也并不简单。
因此,我们首先从较小的数字着手,试算一下。
1234567^1=1234567
1234567^2=1524155677489
1234567^3=恩......
很快数字就变得很大了,试算也很难进行下去了。
且慢,大家要记得现在要求的不是1234567^987654321的乘方,而只是"个位上的数字"。那么,只要找到规律,仅凭笔算就能求出答案哦!
---答案:
能影响两个数字(或者多个数字)乘方结果的个位数的,只有这两个数字的个位数。也就是说,将1234567的个位数7进行乘方,只看乘方结果的个位数就行了,1234567的十位以上的数字123456可以暂且忽略。
我们再来试算一下。
1234567^0的个位=7^0的个位=1
1234567^0的个位=7^1的个位=7
1234567^0的个位=7^2的个位=9
1234567^0的个位=7^3的个位=3 7的3次方等于343
1234567^0的个位=7^4的个位=1
1234567^0的个位=7^5的个位=7
1234567^0的个位=7^6的个位=9
1234567^0的个位=7^7的个位=3
1234567^0的个位=7^8的个位=1
1234567^0的个位=7^9的个位=7
算到这里,就发现规律了。个位是1,7,9,3这四个数字的循环,即周期为4。
由于周期为4,在求1234567^987654321的个位数时,只要用指数987654321除以4算出余数就可以了。987654321除以4的余数为0,1,2,3其中之一,他们分别对应1,7,9,3。

因为987654321除以4余1,所以答案为7。
答案:1234567^987654321的个位数时7。
(2),回顾:规律和余数的关系
要点就是找出规律。只要找出规律,剩下的问题就可以通过余数来解决。
运用余数,大数字的问题就能简化成小数字的问题。
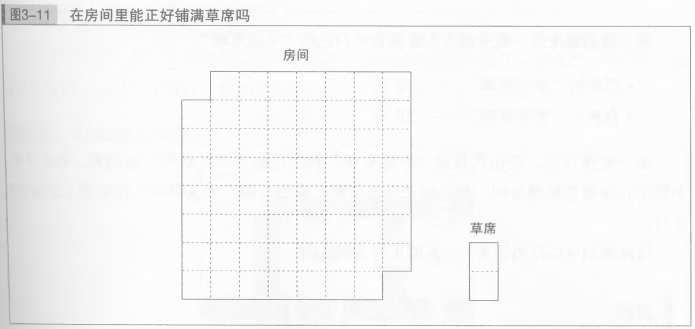
6,铺设草席的思考题(在房间里铺设草席)
有这样一个房间。使用图中右下角所示的草席能够正好铺满房间吗?前提是不能使用半张草席。
如果不能的话,请说明理由。
提示:先计算一下草席数
我们先以半张草席为单位计算一下房间面积。1张草席由2个半张组成,(第一个判断?)如果房间面积按"半张草席"计算得到的结果为奇数,则说明"不能正好铺满"。
计算结果是房间可以铺下62张"半张草席"。可是62是偶数,这就不能光靠其奇偶性来判断能否正好铺满了。
还能找出更好的分类方法吗?
(第二个判断?)以半张草席为单位涂上颜色以示区分。

现在我们就数一数分别有几张黑色和白色的"半张草席"。
* 黑色的"半张草席" 30张
* 白色的"半张草席" 32张
而一整张草席,是由黑色的"半张草席"和白色的"半张草席"组成的。也就是说,不管用几张草席铺满房间,黑色的"半张草席"和白色的"半张草席"在数量上必须相等猜对。
由此我们可以得到答案----不能正好铺满房间。
---回顾总结:
几乎每翻开一本智力书都能看到类似的思考题。原来这个问题也可以通过奇偶校验来解决呢!
如果想通过计算解答,可以进行如下思考:
* 将黑色的"半张草席"的数量记作+1
* 将白色的"半张草席"的数量记作-1
然后将两种"半张草席"的数量相加,再判断计算结果是否为0(1加-1)。如果不是0,就不能正好铺满。不过假如计算结果为0,也并不一定说明能正好铺满。因为"逆命题不一定为真"。
使用这种奇偶校验的判定方法是非常有效的。铺设草席的方法有很多种,要证明"不能铺满"的话,必须罗列出所有情况。然而,只要运用奇偶校验,不用反复试验就能回答"不能"。(程序中也可以这样使用奇偶性判断,而不用反复的试验判断)
这里,希望大家注意的是,要进行有效的奇偶校验,必须找到"合适的分类方法"。例如在铺设草席的问题中,我们为房间的方格涂上了黑白相间的颜色。我们不需要反复试验,需要的是灵感。
@总结:
1,对于难以处理的庞大数值,只要发现其周期性并使用余数,就能够简化问题。
2,通过草席铺设问题,了解到了只要运用奇偶性就能省略反复试验的过程。
3,当我们想要详细地研究事物时,往往容易陷入想正确把握所有细节的思维。但是,像奇偶性校验那般,较之正确的把握,有时准确的分类则更为有效。(不用测试所有的可能,有一个不可能就不可能了。)
4,人们只要发现了周期性和奇偶性,就能将大问题转换为小问题来解决。余数就是其中一种重要的武器。下一章,我们将学习只需两步就能解决无穷问题的方法------数学归纳法。





更多建议: