本文转载至知乎ID:Charles(白露未晞)知乎个人专栏
本文转载至知乎ID:Charles(白露未晞)知乎个人专栏
下载W3Cschool手机App,0基础随时随地学编程>>戳此了解
导语
好几天没推文的罪恶感让我决定今天来水一篇文章。
和之前“Python玩CartPole”那篇推文一样,这也是来自于PyTorch官方教程的一个简单实例。
为了展示我的诚意,我依旧会由浅入深地讲解本文使用到的基本模型:Seq2Seq以及Attention机制。
内容依旧会很长~~~
希望对初入NLP/DeepLearning的童鞋有所帮助~
废话不多说,直接进入正题~~~
相关文件
百度网盘下载链接: https://pan.baidu.com/s/1y3KcMboz_xZJ9Afh5nRkUw
密码: qvhd
参考文献
官方英文教程链接:
http://pytorch.org/tutorials/intermediate/seq2seq_translation_tutorial.html
另外:
对英文文献阅读有困难的同学也不必担心,我已经把这个教程翻译为中文放到了相关文件中。
开发工具
系统:Windows10
Python版本:3.6.4
相关模块:
torch模块;
numpy模块;
matplotlib模块;
以及一些Python自带的模块。
其中PyTorch版本为:
0.3.0
环境搭建
安装Python并添加到环境变量,pip安装需要的相关模块即可。
补充说明:
PyTorch暂时不支持直接pip安装。
有两个选择:
(1)安装anaconda3后在anaconda3的环境下安装(直接pip安装即可);
(2)使用编译好的whl文件安装,下载链接为:
https://pan.baidu.com/s/1dF6ayLr#list/path=%2Fpytorch
原理介绍
PS:
部分内容参考了相关网络博客和书籍。
(1)单层网络
单层网络的结构类似下图:

输入的x经过变换wx+b和激活函数f得到输出y。
相信对机器学习/深度学习有初步了解的同学都知道,这其实就是单层感知机嘛~~~
为了方便起见,我们把它画成这样(请忽视我拙劣的绘图水平):

x为输入向量,y为输出向量,箭头表示一次变换,也就是y=f(Wx+b)。
(2)经典RNN
在实际中,我们会遇到很多序列形的数据:
X1,X2,X3,X4...
例如我们的机器翻译模型,X1可以看作是第一个单词,X2可以看作是第二个单词,以此类推。
原始的神经网络并不能很好地处理序列形的数据,于是救世主RNN出现了,它引入了隐状态h的概念,利用h对序列形的数据提取特征,接着再转换为输出。下面详细说明一下其计算过程(下图中的h0为初始隐藏状态,为简单起见,我们假设它是根据具体模型而设置的一个合理值):
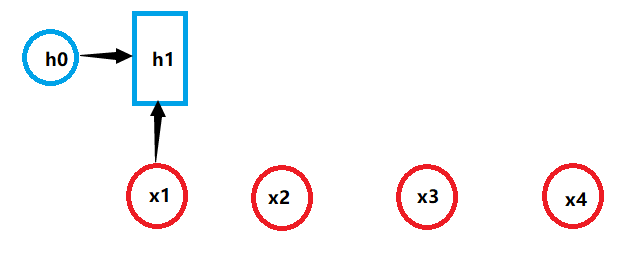
其中:

再重申一遍,所有的字母均为向量,箭头代表对向量做一次变换。
h2的计算与h1类似,并且每一步使用的参数P、Q、b都是一样的,也就是说每个步骤的参数共享:

其中:

以此类推(记住参数都是一样的!!!),该计算可以无限地持续下去(不限于图中的长度4!!!)。
那么RNN的输出又如何得到呢?
RNN的输出值是通过h进行计算的:

其中:

类似地,有y2、y3、y4...:

当然,和前面一样,这里的参数W和c也是共享的。
以上就是最经典的RNN结构,我们可以发现其存在一个致命的缺点:
输入和输出序列必须是等长的!
这个缺点导致了经典RNN的适用范围并没有想象中的那么大。
(3)改进经典RNN
情况1(输入为N,输出为1):
假设我们的问题要求我们输入的是一个序列,输出的是一个单独的数值。那么我们只在最后一个h上进行输出变换就可以了:

情况2(输入为1,输出为N):
当输入只是单一数值而非序列时该怎么办呢?
我们可以只在序列开始进行输入计算:

当然你也可以把输入信息x作为每个阶段的输入:

情况3(输入为N,输出为M):
这是RNN最重要的一个变种,这种结构也被称为:
Encoder-Decoder模型,或者说Seq2Seq模型。
我们的机器翻译模型就是以它为基础的。
Seq2Seq结构先将输入数据编码成一个上下文量c:

其中:

即上下文量c可以直接等于最后一个隐藏状态,也可以是对最后的隐藏状态做一个变换V得到,当然也可以是对所有的隐藏状态做一个变换V得到等等。
上述RNN结构一般称为Encoder。
得到c之后,我们需要另外一个RNN网络对其进行解码操作,即Decoder。你可以把这个c当作初始状态h'0输入到Decoder中:

当然你也可以把c当作Decoder每一步的输入:

算了,补充说明一下吧:
缺少输入的部分(比如某些蓝色的方块没有x输入)你完全可以把x作为0处理然后再代入经典RNN所列出的公式中计算输出,其他的也类似。
(4)Attention机制
在Encoder-Decoder结构中,Encoder把所有的输入序列都编码成一个统一的语义特征c后再进行解码,当输入序列较长时,c很可能无法胜任存储输入序列所有信息的任务。
Attention机制很好地解决了上述问题。它在Decoder每一步输入不同的c:

其中,c根据Encoder中的h生成:

aij代表Encoder中第j阶段的hj和Decoder中第i阶段的相关性。
那么这些权重aij该如何确定呢?aij自然也是从模型中学得的,我们一般认为它与Encoder的第j个阶段的隐状态和Decoder的第i-1阶段的隐状态有关。
比如我们要计算a1j:

然后我们需要计算a2j:

以此类推。
(5)最后任务:法语翻译成英语
有了前面的铺垫,相信大家都能看懂官网的教程。
在这里我们仅做简单的介绍,详细的建模和实现过程可以参考我翻译的官方文档。
Encoder网络为:

Decoder网络为:

其中,encoder最后一个隐藏状态作为decoder的初始隐藏状态。attention机制的权重计算类似(4)中所述。GRU网络的结构为:

GRU网络结构在此就不作详细的介绍了,篇幅太长的话估计没人看得下去吧,就先这样了~~~
在相关文件中我也提供了4篇相关的论文供感兴趣者阅读与研究。(T_T纯英文的~~~)
结果展示
在cmd窗口运行Translation.py文件即可。
误差曲线:

训练过程中cmd窗口的输出:

模型测试:


作为对比:

和最后一个测试结果一模一样有木有!!!
当然,有些翻译结果就不怎么理想了。因为模型和训练数据过于简单了(T_T这里就不举例了)~~~
最后四句话的attention图:




That's all~~~
更多
感兴趣的同学可以进一步修改模型来获得更好的结果,当然也可以找找其他数据集制作诸如中翻英之类的模型~~~





